https://ojs.aaai.org/index.php/AAAI/article/view/25889
Introduction
PUの全般的なサーベイは📄2020-Survey-Learning from positive and unlabeled data: a survey
Sample Selectionでは、Unlabeledの中のPを除外するか重みを減らすことで、実質的にPN学習に帰着させる。
Cost-sensitiveでは、重みつきのPN学習だとみなして学ぶものである。
現状のPU learningが抱えている重大な問題として、Pのデータに過学習して、決定境界がU側に寄る(U側が過剰にPとして扱われてしまう)。
この論文では、Wasserstein距離による理論的解析を行い、その結果をもとにGradientベースの正則化を提案した。また、学習しづらいPositiveには高い損失を付与したらしい。
問題設定
- サンプルはで、Ground-truthのラベルはである。
- Class Priorはである。
- ラベルがついている場合は、付いてない場合はとする。
提案手法
既存のPU learningの問題
与えられたPositiveのサンプルに過学習してしまう。
uPUの学習式は以下の通り。
ここで、について、解きほぐすことになるが、であると考える。つまり、Unlabeledの中のPの分布は、与えられたPのサンプルの分布と違うと仮定する=Domain Shift。
この中で、あきらかにマイナスを含む項で、ある意味矛盾を含む項であるといえる。実際、DNNで学習すると過学習になるので、これを 📄2017-NIPS-[nnPU] Positive-Unlabeled Learning with Non-Negative Risk Estimator のように、max関数で最低でも0と制限することで、ある程度解決できた。ここでの式は以下のように書き直せる。
しかし、それでも、訓練の早期段階でNegative in Unlabeledがうまく学習できていないときは、が大きくなり、の最適化になっている。もし、PositiveとPositive in Unlabeledが同じものならばこれの最適化は0になってしかるべきであるが、分布が違う=選択バイアスがあると、overfittingをして学習がゆがんでしまうのではないか。
Sample Selectionの手法でも、やはり一部の識別境界に近いNegative in Unlabeledがあいまいだということで、排除されてしまうという問題を抱えている。
Positiveへの過学習
DNNは学習能力が高いので、PositiveとPositive in Unlabeledの分布が一致しないとき、一致しないままで学習して過学習をしてしまうというものである。
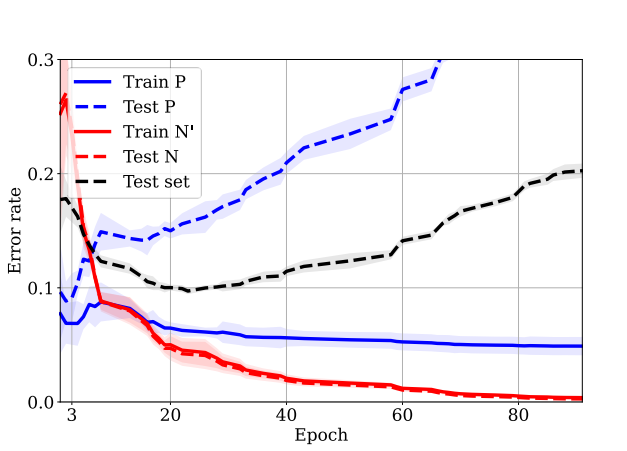
この図のように、TrainやTest問わずにNegative in Unlabeledが学習されていく。そして、Positive in Unlabeled(これあってる?与えられたPositiveとPositive in Unlabeled両方かも?)の学習が遅い上過学習しており、実際にはTest DataのPositiveのAccuracyが下がっていく。
📄2023-NIPS-Beyond Myopia: Learning from Positive and Unlabeled Data through Holistic Predictive Trends にもあるように、識別境界がPositive側に食い込みすぎてしまうNegative Assumptionがある。
Wasserstein距離による誤差上界
を1次元ワッサースタイン距離=つまり普通のコストがすべて等しいときの最適輸送問題であるとする。双対によって、以下のことが成り立つ。はの最小のリプシッツ定数(最小のってなんだよ)
また、以下のように設定する。
すると、以下の式が成り立つ。これ自体はTaraglandの補題を応用して、リプシッツ定数を外に出して評価しているもの。は理想のデータの分布、は経験分布。つまり、でTalagrandの補題をつかい、集中不等式ではなくWasserstein距離による上界評価である。
これを用いることで、以下の定理が成り立つ。
絶対値損失関数と、任意のリプシッツ連続なを考える。Labeled PositiveがSCAR仮定に従うと、以下のように誤差上界が決まる。
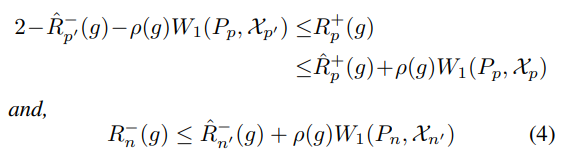
- はがPositive in Unlabeledであり、それについてのについての経験リスク。
- はPositive in Unlabeledの経験分布である。
- は真のPositive分布における損失の和。
第2式は、同じについての損失でも、真のNegativeの分布による損失と、Negative in Unlabeledの経験損失はWasserstein距離で抑えられるということ。
これらの結果から以下のことが言える。
- 訓練データがよく学習できている場合、などが小さいということである。この時、誤差上界を支配するのは一次のWasserstein距離とリプシッツ定数?である。
- Wasserstein距離自体はDomain Shiftにおける評価指標なので、Domainが変わらない場合、が小さい、つまり損失関数と識別器のgradientが小さいほうが望ましい。
- 真のPositiveの分布と、Positive in UnlabeledにDomain Shiftが生じて、矛盾するようなDomain Shiftが得られた(間違ったラベルとか)とすると、識別器はなめらかではなくなりGradientが大きくなる。
実際のところ、以下のようにPやP in Uに大きなGradient Normが生まれている。これはがPやP in Uにおいて大きいという証拠である。与えたPのクラスで、できるだけ強いラベルの一貫性が欲しいってことかな。
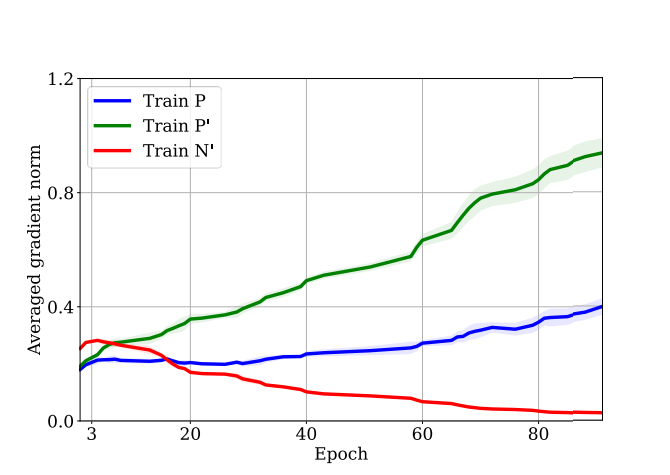
- が小さければ小さいほどいいわけでもない。小さすぎると、誤差上界の左辺はが支配的になるということ。これが意味するものは、P in Uを完璧に学習したときに、Pはほぼ間違える=上界2の近くまで伸びうるということ。
- P in Uの学習と、Pの学習は上界から見るとトレードオフになっている。
提案手法
Gradientベースの正則化=Gradient Penaltyを加える。は、PとUからハイパーパラメタの割合でとは関係がないっぽい。
もし、過学習しない前提で小さい勾配を持った識別器によって訓練できるのならば、このGradient Penaltyはそうなるように仕向けられる。
Pの訓練損失が増大することから、それを抑えるためにPの重みを大きくして減らす重要度を挙げてみる。
これについて、識別器がと予測するほど少しだけ重みが増え、に近い予測ほど大きく重みが増える。AdaBoostの式。
全体的な学習の式は以下の通り。この式はnnPUとかのClass Priorを捨てて、AdaBoostにすべてを任せて学習していると考えられる。
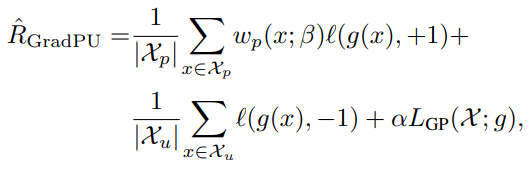
損失関数は単純ににしている。
アルゴリズム

- 各ミニバッジごとに以下のように学習する。
- Gradient Penaltyを計算するためのを一様分布から得る。
- Gradient Penaltyを計算。
- Adaboostのアルゴリズムを使って、Pの重みを計算。
- そこで使われるはAdaBoostの知見により、訓練とおなじタイミングで線形に増加をさせていく。
- 訓練の後ろの方になればなるほど、大きく損失の重みの差がつけられるようにする。
実験とその結果
- Gradient Penaltyは効果ある。妥当なAlphaを選ぶ限り。

- ほかの正則化、weight decay, dropout, mix-up, network boundと比較してもGradient Penaltyのほうがよかった。
- AdaBoostのアルゴリズム通り、は線形に増やすべきですね。これがないと性能が壊れる。
- 選択バイアスがあるとき、📄
2019-ICLR-[PUSB]Learning from Positive and Unlabeled Data with a Selection Bias +nnPUと比べても、こっちのほうがよかったですね。
